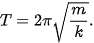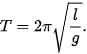(Trang 20)
| Ở lớp 10, khi học về chuyển động của vật, ta đã biết có sự chuyển hoá giữa động năng và thế năng của vật. Vậy trong dao động điều hoà, có sự chuyển hoá tương tự không? |
I. ĐỘNG NĂNG
| – Động năng của vật dao động điều hoà được xác định bởi biểu thức:
Công thức (5.1) cho biết sự biến thiên của động năng theo li độ x. |
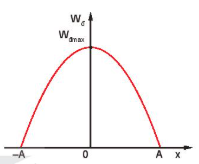
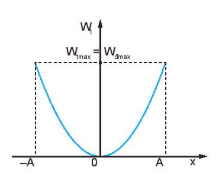
Hình 5.1. Sự biến thiên của động năng |
– Hình 5.1 là đồ thị chỉ sự biến thiên của động năng theo li độ x. Đó là một đường parabol có bề lõm hướng xuống và có giá trị cực đại: 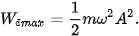
Đồ thị cho thấy, khi vật đi từ vị trí cân bằng tới vị trí biên thì động năng của vật đang từ cực đại giảm đến 0. Khi vật đi từ vị trí biên về vị trí cân bằng thì động năng của vật tăng từ 0 đến giá trị cực đại.
II. THẾ NĂNG
| – Theo định luật bảo toàn năng lượng, nếu bỏ qua ma sát thì động năng của vật không mất đi mà chuyển dần thành thế năng của vật và ngược lại. Vì thế ta có thể viết:
Công thức (5.2) cho biết sự biến thiên của thế năng theo li độ. |
Hình 5.2. Sự biến thiên của thế năng |
– Đồ thị biến thiên của thế năng theo li độ x cũng là một đường parabol nhưng bề lõm hướng lên như Hình 5.2 và có giá trị cực đại: 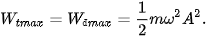
(Trang 21)
III. CƠ NĂNG
Trong dao động điều hoà, có sự chuyển hoá qua lại giữa động năng và thế năng của vật, còn cơ năng, tức tổng động năng và thế năng thì được bảo toàn.
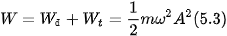
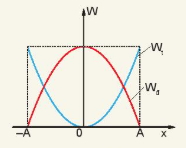
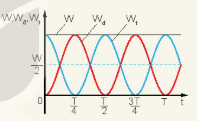
| 1. Hình 5.3 là đồ thị động năng và thế năng của một vật dao động điều hoà theo li độ. Hãy phân tích sự chuyển hoá giữa động năng và thế năng bằng đồ thị. 2. Hình 5.4 là đồ thị động năng, thế năng và cơ năng của một vật dao động điều hoà theo thời gian. a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến b) Tại các thời điểm: |
Hình 5.3
Hình 5.4 |
IV. CƠ NĂNG CỦA CON LẮC LÒ XO VÀ CON LẮC ĐƠN
1. Con lắc lò xo
Ta biết nếu bỏ qua ma sát thì dao động của con lắc lò xo là dao động điều hoà.
Người ta đã chứng minh được rằng, nếu chọn mốc thế năng ở vị trí cân bằng thì thế năng của con lắc lò xo khi vật ở li độ x là:
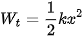 | (5.4) |
với k là độ cứng của lò xo.
So sánh (5.4) với (5.2) ta suy ra 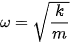 và chu kì của con lắc lò xo là:
và chu kì của con lắc lò xo là:
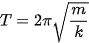 | (5.5) |

Hình 5.5. Con lắc lò xo
(Trang 22)
Theo công thức 5.3 thì cơ năng của con lắc lò xo là:
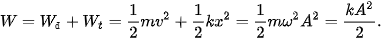
2. Con lắc đơn
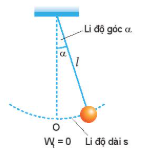
| – Vị trí của con lắc đơn được xác định bằng li độ dài s hay li độ góc α (Hình 5.6). – Thế năng của con lắc đơn là thế năng trọng trường. Chọn mốc thế năng ở vị trí cân bằng thì thế năng của con lắc ở li độ góc α là :
Có thể chứng minh được rằng, khi góc α nhỏ (sinα ≈ α rad) thì
So sánh (5.7) với (5.2) ta suy ra: Khi góc lệch α nhỏ (sinα ≈ a), con lắc đơn dao động điều hoà với tần số góc
|
Hình 5.6. Con lắc đơn Li độ góc α Li độ dài s
Làm thí nghiệm để xác nhận rằng khi góc lệch |
Hãy chứng minh rằng, khi góc lệch α nhỏ (sinα ≈ α rad) thì công thức (5.6) trở thành (5.7).
Một con lắc lò xo có độ cứng k và vật nặng có khối lượng m.
1. Tính chu kỳ T.
2. Đo chu kỳ T bằng đồng hồ. So sánh kết quả thu được với kết quả tính ở câu 1.
(Trang 23)
| 1. Một con lắc lò xo có vật nặng khối lượng 0,4 kg, dao động điều hoà. Đồ thị vận tốc v theo thời gian t như Hình 5.7. Tính: a) Vận tốc cực đại của vật. b) Động năng cực đại của vật. c) Thế năng cực đại của con lắc. d) Độ cứng k của lò xo. |
Hình 5.7 |
2. Một con lắc lò xo gồm lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 200 g, dao động điều hoà với biên độ A = 5 cm. Xác định:
a) Li độ của vật tại thời điểm động năng của vật bằng ba lần thế năng của con lắc.
b) Tốc độ của vật khi vật qua vị trí cân bằng.
c) Thế năng của con lắc khi vật có li độ x = – 2,5 cm.
| EM ĐÃ HỌC • Một vật có khối lượng m dao động điều hoà với tần số góc α và biên độ A. Tại li độ x: – Động năng của vật là: – Thế năng của vật là: • Cơ năng của vật là: • Con lắc lò xo dao động điều hòa với chu kì • Con lắc đơn với góc lệch nhỏ (a ≤ 10°) dao động điều hoà với chu kì |
| EM CÓ THỂ • Phân tích được sự chuyển hoá giữa động năng và thế năng trong dao động điều hoà ở một số ví dụ trong đời sống. |
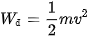 . Thay
. Thay 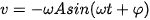 vào, ta được:
vào, ta được: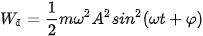
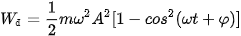
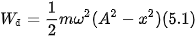
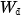 theo li độ x
theo li độ x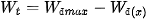
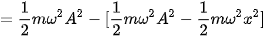
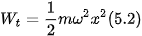
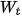 theo li độ x
theo li độ x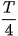 , từ
, từ 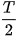 , từ
, từ 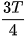 , từ
, từ 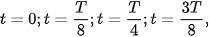 động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó
động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó 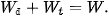
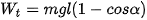
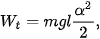 thay
thay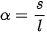 vào ta được:
vào ta được: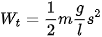
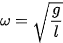

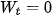
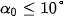 thì chu kì của con lắc đơn gần như không phụ thuộc vào
thì chu kì của con lắc đơn gần như không phụ thuộc vào 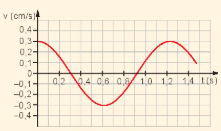
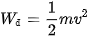
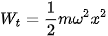
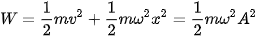 = hằng số
= hằng số