(Trang 9)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
| Khi diễu hành, để đội hình được giữ vững, ở mỗi bước, những người tham gia cần tiến đều nhau về cùng một hướng. Điều này có gì liên quan tới Toán học? |
Khối hồng kì trong Đại lễ kỉ niệm 1000 năm |
1. PHÉP TỊNH TIẾN
| >HĐ1. Ở mỗi bước của đội hình diễu hành, gọi vectơ dịch chuyển của mỗi người tham gia là vectơ có điểm gốc và điểm ngọn tương ứng là vị trí trước và sau khi bước của người đó. Để giữ vững đội hình, ở mỗi bước, các vectơ dịch chuyển của những người tham gia cần có mối quan hệ gì với nhau? |
Hình 1.5 |
Cho vectơ 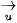 . Phép biến hình biến mỗi điểm M thành điểm M' sao cho . Phép biến hình biến mỗi điểm M thành điểm M' sao cho 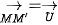 gọi là phép tịnh tiến theo gọi là phép tịnh tiến theo 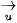 , kí hiệu , kí hiệu 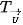 . Vectơ . Vectơ 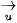 được gọi là vectơ tịnh tiến. được gọi là vectơ tịnh tiến. |
Chú ý. Phép tịnh tiến theo vectơ 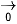 là phép đồng nhất.
là phép đồng nhất.
? Nếu phép tịnh tiến 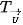 biến điểm M thành điểm M' thì phép tịnh tiến
biến điểm M thành điểm M' thì phép tịnh tiến 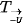 biến điểm M' thành điểm nào?
biến điểm M' thành điểm nào?
(Trang 10)
>Ví dụ 1. Trong mặt phẳng toạ độ Oxy, xác định phép tịnh tiến biến điểm A(1, 2) thành điểm A'(2, 5).
Giải
Giả sử phép tịnh tiến theo vectơ 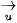 biến điểm A(1, 2) thành A'(2; 5). Khi đó
biến điểm A(1, 2) thành A'(2; 5). Khi đó 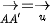 . Mặt khác,
. Mặt khác, 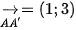 nên
nên 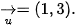 . Vậy phép tịnh tiến biến A(1; 2) thành điểm A'(2, 5) là phép tịnh tiến theo vecto
. Vậy phép tịnh tiến biến A(1; 2) thành điểm A'(2, 5) là phép tịnh tiến theo vecto 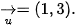
>Luyện tập 1. Trong Hình 1.6, tìm ảnh của các điểm M, N, P, Q, B qua phép tịnh tiến theo 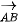
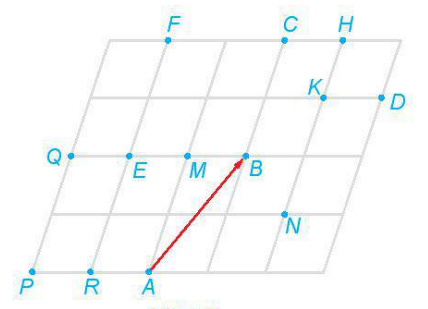
Hình 1.6
>Vận dụng 1. Bạn Hùng tham gia vào một khối diễu hành. Trong khi diễu hành, mỗi bước Hùng tiến về hướng đông 30 cm. Để giữ vững đội hình, sau mỗi bước, tất cả mọi người tham gia trong khối diễu hành của Hùng cần dời tới vị trí mới là ảnh của vị trí cũ qua phép biến hình nào?
2. TÍNH CHẤT
>HĐ2. Phép tịnh tiến 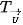 biến M thành M', N thành N' (H.1.7).
biến M thành M', N thành N' (H.1.7).
a) Có nhận xét gì về 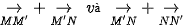
b) Tìm mối quan hệ giữa hai vectơ 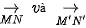 .
.
Nếu phép tịnh tiến biến các điểm M, N tương ứng thành các điềm M', N' thì 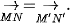 Vậy phép tịnh tiến bảo toàn khoảng cách giữa hai điểm. Vậy phép tịnh tiến bảo toàn khoảng cách giữa hai điểm. |
Từ tính chất trên, ta có thể rút ra:
| Phép tịnh tiến biến:
|
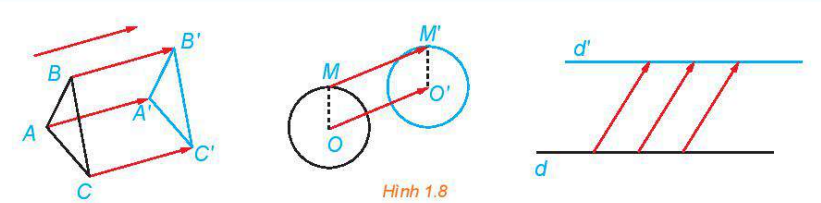
(Trang 11)
| >Ví dụ 2. Cho tam giác ABC và M, N, P tương ứng là trung điểm của các cạnh BС, CА, АВ. Tìm ảnh của tam giác BMP qua các phép tịnh tiến Giải (H. 1.9) Vì Vì | 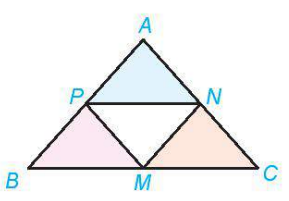 |
>Luyện tập 2. Cho đường tròn (O; R) và điểm O' khác điểm O. Với mỗi điểm M thuộc (O; R) sao cho O, O', M không thằng hàng, vẽ hình bình hành MOO'M'. Hỏi khi M thay đổi trên (O; R) thì M' thay đổi trên đường nào?
>Vận dụng 2. Trong việc lát mặt phẳng bởi các tam giác đều bằng nhau như được thể hiện trong Hình 1.10, phép tịnh tiến theo vectơ 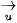 có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không? có biến mỗi viên gạch màu xanh thành một viên gạch màu xanh, mỗi viên gạch màu đỏ thành một viên gạch màu đỏ hay không? |
Hình 1.10 |
BÀI TẬP
1.3. Cho 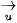 là một vectơ chỉ phương của đường thẳng
là một vectơ chỉ phương của đường thẳng  . Hỏi phép tịnh tiến
. Hỏi phép tịnh tiến 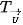 biến
biến  thành đường thẳng nào?
thành đường thẳng nào?
1.4. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x - 1)2 +(y + 2)2 = 25 và vecto 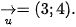 .
.
a) Xác định ảnh của tâm đường tròn (C) qua phép tịnh tiến 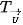
b) Viết phương trình đường tròn (C') là ảnh của (C) qua 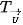
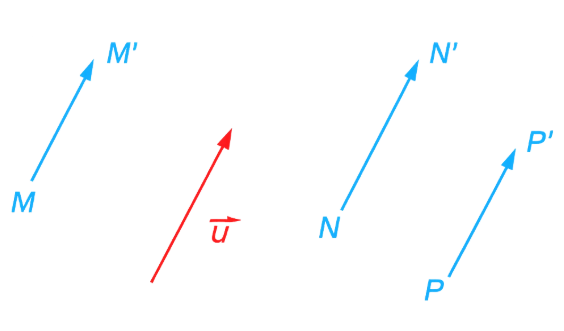
1.5. Trong việc lát sàn nhà như Hình 1.11, viên gạch ở hàng dọc thứ 4 từ trái sang và hàng ngang thứ 2 từ dưới lên là ảnh của viên gạch ở góc dưới bên trái qua phép tịnh tiến theo vecto nào? (Gợi ý: Tính vecto tịnh tiến đó theo hai vecto 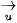 ,
, 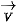 trên hình vẽ).
trên hình vẽ).

Hình 1.11

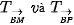
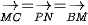 nên phép tịnh tiến
nên phép tịnh tiến 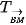 biến các điểm B, M, P tương ứng thành M, C, N. Do đó,
biến các điểm B, M, P tương ứng thành M, C, N. Do đó, 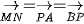 nên phép tịnh tiến
nên phép tịnh tiến 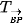 biến các điểm B, M, P tương ứng thành P, N, A. Do đó,
biến các điểm B, M, P tương ứng thành P, N, A. Do đó, 

























