(Trang 85)
Ví dụ 1
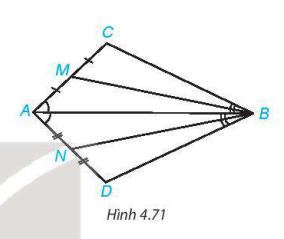
Cho hình 4.71, biết ∠ABC = ∠ABD, ∠BAC = ∠BAD.
Gọi M , N lần lượt là trung điểm của các đoạn thẳng AC, AD. Chứng minh rằng:
a) 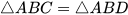 ; b)
; b) 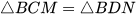 .
.
Giải
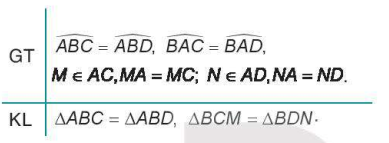
a) Hai tam giác ABC và ABD có:
∠ABC = ∠ABD (theo giả thiết);
AB là cạnh chung;
∠BAC = ∠BAD (theo giả thiết).
Vậy 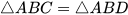 (g.c.g).
(g.c.g).
b) Vì 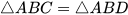 (theo chứng minh trên) nên BC = BD, AC = AD và ∠BCA = ∠BDA.
(theo chứng minh trên) nên BC = BD, AC = AD và ∠BCA = ∠BDA.
Do M, N lần lượt thuộc CA, DA nên ∠BCM = ∠BCA, ∠BDN = ∠BDA.
Vì vậy ∠BCM = ∠BCA = ∠BDA = ∠BDN.
Mặt khác, vì M và N lần lượt là trung điểm của AC và AD nên 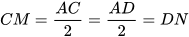 .
.
Vậy hai tam giác BCM và BDN có:
BC = BD, ∠BCM = ∠BDN, CM = DN (theo chứng minh trên).
Do đó 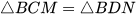 (c.g.c).
(c.g.c).
Ví dụ 2
Cho d là đường trung trực của đoạn thẳng AB và O là giao điểm của d với AB. Cho M và N là hai điểm phân biệt nằm trên d sao cho OM = ON. Chứng minh rằng:
a) 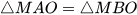 ;
;
b) ∠MAN = ∠MBN;
c) Tam giác AMN cân tại A.
(Trang 86)

Vì d là đường trung trực của đoạn thẳng AB nên d vuông góc với AB tại O.
a) Xét hai tam giác vuông MAO và MBO. Ta có:
OM là cạnh chung; AM = BM (vì M thuộc đường trung trực của đoạn thẳng AB).
Do đó 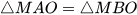 (cạnh huyền - cạnh góc vuông).
(cạnh huyền - cạnh góc vuông).
b) Xét hai tam giác MAN và MBN. Ta có:
MA = MB (vì M thuộc đường trung trực của đoạn thẳng AB);
NA = NB (vì N thuộc đường trung trực của đoạn thẳng AB);
MN là cạnh chung.
Vậy 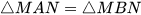 (c.c.c).
(c.c.c).
Do đó ∠MAN = ∠MBN (hai góc tương ứng).
c) Xét hai tam giác vuông AOM và AON. Ta có:
OM = ON (theo giả thiết); OA là cạnh chung.
Do đó 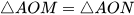 (hai cạnh góc vuông).
(hai cạnh góc vuông).
Vậy AM = AN (hai cạnh tương ứng). Từ đó suy ra tam giác AMN cân tại A.
BÀI TẬP
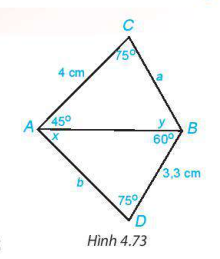
4.29. Cho hình 4.73. Hãy tìm số đo x, y của các góc và độ dài a, b của các đoạn thẳng trên hình vẽ.
4.30. Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.
Chứng minh rằng:
a) 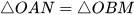 ; b)
; b) 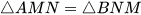 .
.
4.31. CHo hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
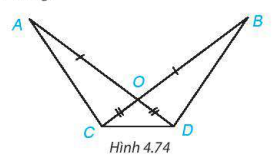
a) AC = BDl b) 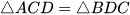 .
.
4.32. Cho tam giác MBC vuông tại M có ∠B = 60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

























