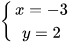(Trang 111)
| Mục tiêu Sử dụng phần mềm GeoGebra để vẽ đồ thị của hàm số, giải phương trình một ẩn và giải hệ hai phương trình bậc nhất hai ẩn. |
Khởi động phần mềm GeoGebra  , chọn Complex Adaptive System (CAS) để thực hiện giải phương trình một ẩn và hệ hai phương trình bậc nhất hai ẩn; chọn Graphic 2 để vẽ đồ thị của hàm số.
, chọn Complex Adaptive System (CAS) để thực hiện giải phương trình một ẩn và hệ hai phương trình bậc nhất hai ẩn; chọn Graphic 2 để vẽ đồ thị của hàm số.
1 GIẢI PHƯƠNG TRÌNH MỘT ẨN
Để giải phương trình nói chung, phương trình bậc hai một ẩn nói riêng, ta dùng lệnh Solve(<phương trình>) hoặc Solutions(<phương trình>) trên ô lệnh của cửa sổ CAS, kết quả sẽ được hiển thị ngay bên dưới.

Nghiệm của phương trình được biểu diễn dưới dạng tập hợp. Chú ý, kí hiệu {} thể hiện phương trình vô nghiệm.

(Trang 112)

Chú ý.
• Để nhập căn bậc hai của a ta gõ "sqrt(a)".
• Để nhập 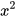 ta gõ "x^2".
ta gõ "x^2".
2 GIẢI HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Để giải hệ hai phương trình bậc nhất hai ẩn, ta có thể sử dụng một trong hai phương pháp sau:
Cách 1. Sử dụng câu lệnh Solve({<phương trình thứ nhất>, <phương trình thứ hai>}, {<biến số thứ nhất>, <biến số thứ hai>}) hoặc Solutions({<phương trình thứ nhất, <phương trình thứ hai>}, {<biến số thứ nhất>, <biến số thứ hai>}) trên ô lệnh của cửa sổ CAS, kết quả sẽ được hiển thị ngay bên dưới.
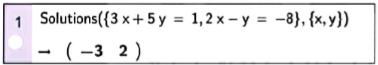 | Kết quả bên có nghĩa: hệ có nghiệm |
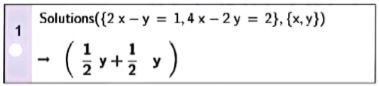 | Kết quả bên có nghĩa: hệ có nghiệm 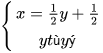 |
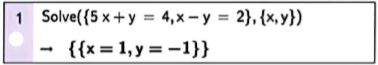 | |
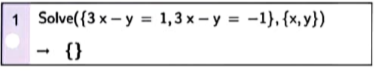 |
Cách 2. Sử dụng lệnh Intersect (<phương trình thứ nhất>, <phương trình thứ hai) trên cửa sổ CAS để tìm toạ độ giao điểm của hai đường thẳng có phương trình tương ứng.
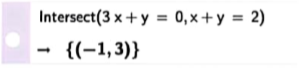
(Trang 113)
3 VẼ ĐỒ THỊ CỦA HÀM SỐ
Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số y = a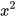 (a ≠ 0) và hàm số bậc nhất y = ax + b (a ≠ 0).
(a ≠ 0) và hàm số bậc nhất y = ax + b (a ≠ 0).
– Nhập công thức hàm số y = a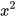 và y = ax + b vào từng ô lệnh trong cửa sổ CAS.
và y = ax + b vào từng ô lệnh trong cửa sổ CAS.
– Nháy chuột chọn nứt  ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
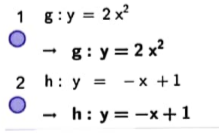 | 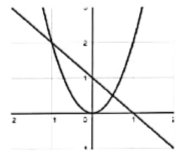 |
– Sử dụng lệnh Intersect (<hàm số thứ nhất>, <hàm số thứ hai>) trên cửa sổ CAS. Toạ độ các giao điểm của hai đồ thị hàm số sẽ hiển thị bên dưới ở dạng tập hợp.
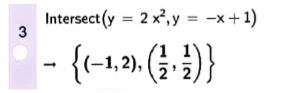
Chú ý. Nếu muốn sử dụng giao diện tiếng Việt, sau khi khởi động GeoGebra, chọn Options → Language → Vietnamese/Tiếng Việt. Khi đó, thay vì cú pháp lệnh tiếng Anh như trình bày ở trên, ta dùng cú pháp lệnh tiếng Việt tương ứng như trong bảng sau (lưu ý rằng cú pháp lệnh tiếng Việt có thể khác nhau tuỳ theo phiên bản GeoGebra).
| Lệnh | Cú pháp lệnh tiếng Anh | Cú pháp lệnh tiếng Việt |
| Giải phương trình | Solve(<phương trình>) | Giai(<phương trình>) |
| Solutions(<phương trình>) | CacNghiem(<phương trình>) | |
| Giải hệ phương trình | Solve({<phương trình thứ nhất>, <phương trình thứ hai>}, {<biến số thứ nhất>, <biến số thứ hai>}) | Giai({<phương trình thứ nhất>, <phương trình thứ hai}, {<biến số thứ nhất>, <biến số thứ hai>}) |
| Solutions({<phương trình thứ nhất>, <phương trình thứ hai>}, {<biến số thứ nhất>, <biến số thứ hai>}) | CacNghiem({<phương trình thứ nhất>, <phương trình thứ hai}, {<biến số thứ nhất>, <biến số thứ hai>}) | |
| Tìm giao điểm của hai đồ thị | Intersect (<hàm số thứ nhất>, <hàm số thứ hai>) | GiaoDiem (<hàm số thứ nhất>, <hàm số thứ hai>) |
(Trang 114)
THỰC HÀNH
Sử dụng phần mềm GeoGebra thực hiện các yêu cầu sau:
1. Giải các phương trình sau:
a) 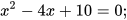 b)
b) 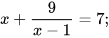
c) 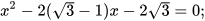 d)
d) 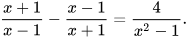
2. Giải các hệ phương trình sau:
a) 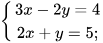 b)
b) 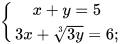
c) 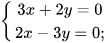 d)
d) 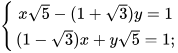
3. Cho đường thẳng (d): 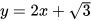 và parabol (P): y =
và parabol (P): y = 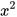 .
.
a) Vẽ đường thẳng (d) và parabol (P) trên cùng một mặt phẳng toạ độ.
b) Tìm toạ độ giao điểm của (d) và (P).